机器学习深度学习李宏毅版-学习笔记

Qifei

学习笔记

发布于：2020年5月21日

次浏览

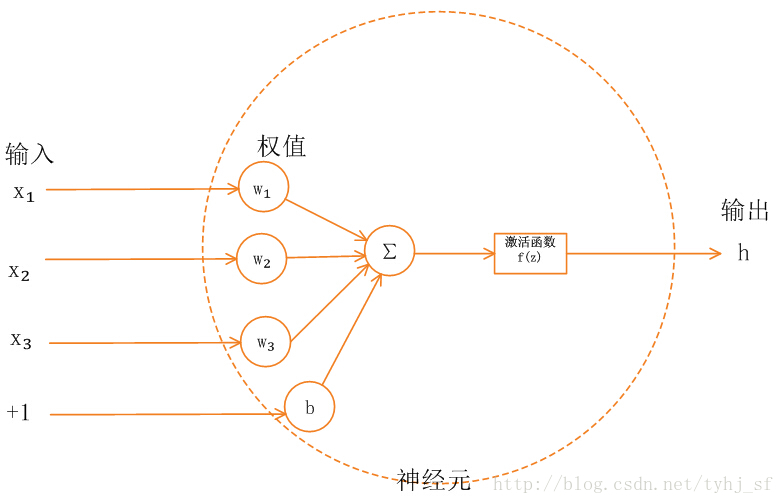
第一章 Regression 回归

$$
f(input)=output
$$

输入一个对象后，有指定的输出结果。

示例应用：数码宝贝原始cp值，求进化一次后的cp值

Step 1: Model

定义一个函数：确定输入原始cp值和输出进化后的cp值。
$$
y=b+w*x_{cp}
$$

w and b are parameters

Step 2: Goodness of Function方程好坏

对象1：function input: cp612->x1 function output:cp979->y1
$$
(x^1,y^1)
$$

$$
(x^2,y^2)
$$

$$
……
$$

$$
(x^{10},y^{10})
$$

定义另一个函数：确定第一个函数效果如何。输入一个函数，输出函数好坏程度。

Loss Function
$$
\begin{split}
L(f) &= L(w,b)
\ &=\sum_{n=1}^{10}\left(y^n-\left(b+w*x^n_{cp}\right)\right)^2
\end{split}
$$
Step 3: Best Function最好的函数

Gradient Descent
$$
w^*=arg\ min\ L(w)
$$
枚举w值，找到Loss Function最小的w值。

随机选择一个初始w0,
$$
\frac{dL}{dw}|w=w^0
$$

在w0位置，如果斜率为正，则w向小的位置移动，反之向w增大的位置移动，目的是找到L(w)更小的位置。下一个位置w1。
$$
w^1=w^0-\eta\frac{\partial L}{\partial w}|w=w^0,b=b^0
\b^1=b^0-\eta\frac{\partial L}{\partial b}|w=w^0,b=b^0
\\eta表示学习率。
$$
最终找到一个最佳的w和b，确定一个L(f)最小。

然而，由于数码宝贝的物种不同，b和w的取值将不同。

修改模型

Step 1:选择模型
$$
y=b_1\delta(x^s=宝贝1)+w_1\delta(x_s=宝贝1)x_{cp}+b_2\delta(x^s=宝贝2)+w_2*\delta(x_s=宝贝2)*x_{cp}+……
$$

$$
\delta(x_s=宝贝1)\begin{cases}
=1\ if,x_s=宝贝1 \\
=0\ else\end{cases}
$$

此时已经很精准了，但是可能还存在其他除了种类以外的影响因素，比如身高，体重，hp。

回到Step 2:Regularization
$$
y=b+\sum w_ix_i
\L=\sum_n(y^n-(b+\sum w_ix_i))^2+\lambda\sum (w_i)^2
$$
为了获取一个更光滑的曲线，来减少噪音对输出结果的影响。

采用较小的拟合次数简单的model，通常具有更小的方差，但偏差更大，即结果集中但集中位置偏离真实值；较大的拟合次数复杂的model，方差比较大，但偏差更小。

偏差大：

更多训练数据
更复杂的模型

方差大：

更多训练数据

获取模型：Validation

训练数据->分三份，两份获取模型，一份验证模型。

第二章 Gradient Descent梯度下降法

在第一章Step 3中，我们要找到一个最低的loss function
$$
\theta^*=arg\ max\ L(\theta) \ \ \ \ L:loss\ function\ \ \theta:parameters
$$
假设$\theta$有两个参数${\theta_1,\theta_2}$

随机设置一个$\theta^0=\begin{bmatrix}\theta_1^0\\theta_2^0\end{bmatrix}$
$$
\begin{bmatrix}\theta_1^1\\theta_2^1\end{bmatrix}=\begin{bmatrix}\theta_1^0\\theta^0_2\end{bmatrix}-\eta\begin{bmatrix}\frac{\partial(\theta_1^0)}{\partial\theta_1}\\frac{\partial(\theta_2^0)}{\partial\theta_2}\end{bmatrix}
$$

$$
\begin{bmatrix}\theta_1^2\\theta_2^2\end{bmatrix}=\begin{bmatrix}\theta_1^1\\theta^1_2\end{bmatrix}-\eta\begin{bmatrix}\frac{\partial(\theta_1^1)}{\partial\theta_1}\\frac{\partial(\theta_2^1)}{\partial\theta_2}\end{bmatrix}
$$

简化公式：
$$
\bigtriangledown L(\theta)=\begin{bmatrix}\frac{\partial L(\theta_1)}{\partial\theta_1}\\frac{\partial L(\theta_2)}{\partial\theta_2}\end{bmatrix}
\\theta^1=\theta^0-\eta\bigtriangledown L(\theta^0)
$$
需要调节学习率（步长）$\eta$到合适的值。

不同的$\theta$给不同的$\eta$。

Adagrad:随着参数增加，步长逐渐减小。
$$
w^1\gets w^1-\frac{\eta^0}{\sigma^0}g^0 \ \ \ \sigma^0=\sqrt{(g^0)^2}
\\vdots
\\vdots
\w^{t+1}\gets w^t-\frac{\eta^t}{\sigma^t}g^t\ \ \ \sigma^t=\sqrt{\frac{1}{t+1}\sum^t_{i=0}(g^i)^2}
$$

$$
\eta^t=\frac{\eta}{\sqrt{t+1}}
$$

Feature Scaling:

将多个x输入的范围统一到一个范围，以保证在计算L(f)时，每个w对L(f)的影响相同。

Gradient Descent会卡在局部最小值的位置

第三章 New Optimizers for Deep Learning 优化

一些记号：

$\theta_t$:模型参数

$m_{t+1}$:从step 0到step t 的动量。

SGD：

SGDM、Learning rate scheduling、NAG

走到最低点时，还不会停下来，由于之前的动量影响，存在一个类似的惯性作用，会继续向上爬坡。

Adam：

Adagrad、RMSProp、AMSGrad、AdaBound、RAdam、Nadam、AdamW

SGD+Adam->SWATS

Lookahead

第四章 Classification 分类

例：投简历

输入：收入、存款、专业、年纪
输出：录取或拒绝

模型：
$$
x\rightarrow f(x)\begin{cases}g(x)>0\ &Output=class1\else \ \ &Output=class2\end{cases}
$$
Loss function：
$$
L(f)=\sum_n\delta(f(x^n)\ne y^n)
$$
79个水系（C1）宝可梦，61只普通系（C2）的宝可梦

$P(x|C_1)$的可能性。

$P(x|C_1)$满足高斯分布（正态分布），找到最合适的高速分布系数$\mu$和$E$

使用贝叶斯公式，求测试数据$P(C_1|x)$的概率。

所以：

模型
$$
x\rightarrow P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)}
$$
函数的好坏：

平均值$\mu$和$E$。

一堆数学运算……

模型：
$$
P_{w,b}(C_2|x)=\sigma(z)
\
\sigma(z)=\frac{1}{1+exp(-z)}
\
z=w*x+b
$$

第五章 Logistic Regression

$$
f_{w,b}(x)=\sigma(\sum w_ix+b)
$$
$x_1$属于$C_1$,$x_2$属于$C_1$,$x_3$属于$C_2$……
$$
L(w,b)=f_{w,b}(x^1)f_{w,b}(x^2)(1-f_{w,b}(x^3))…
$$
找到一个$w^*,b^*$满足$arg\ max,L(w,b)$最大。

第六章 Deep learning

历史：

1958: Perceptron(linear model)

1980: Multi-layer perceptron

1986: Backpropagation

1989: 1 hidden layer is “good enough”

2006: RBM initialization

2009: GPU

2011: Speech recognizition

步骤：

找到一个函数->Neural Network

Deep = Many hidden layers

第七章 Backpropagation 反向传播

让计算梯度下降法的参数更有效。

Chain Rule 链式法则：

Case1：
$$
y=g(x) \ \ \ \ z=h(y)
\\triangle x \rightarrow \triangle y\rightarrow \triangle z
\ \frac{dz}{dx}=\frac{dz}{dy}\frac{dy}{dx}
$$
Case2:
$$
x=g(s) \ \ y=h(s) \ \ z=k(x,y)
\ \frac{dz}{ds}=\frac{\partial z}{\partial x}\frac{dx}{ds}+\frac{\partial z}{\partial y}\frac{dy}{ds}
$$

Loss function是所有输入经神经网络处理后的输出，与理想输出误差之和。
$$
L(\theta)=\sum_nC(\theta)
$$
对Loss function求导：
$$
\frac{\partial L}{\partial w}=\sum_n\frac{\partial C}{\partial w}
$$
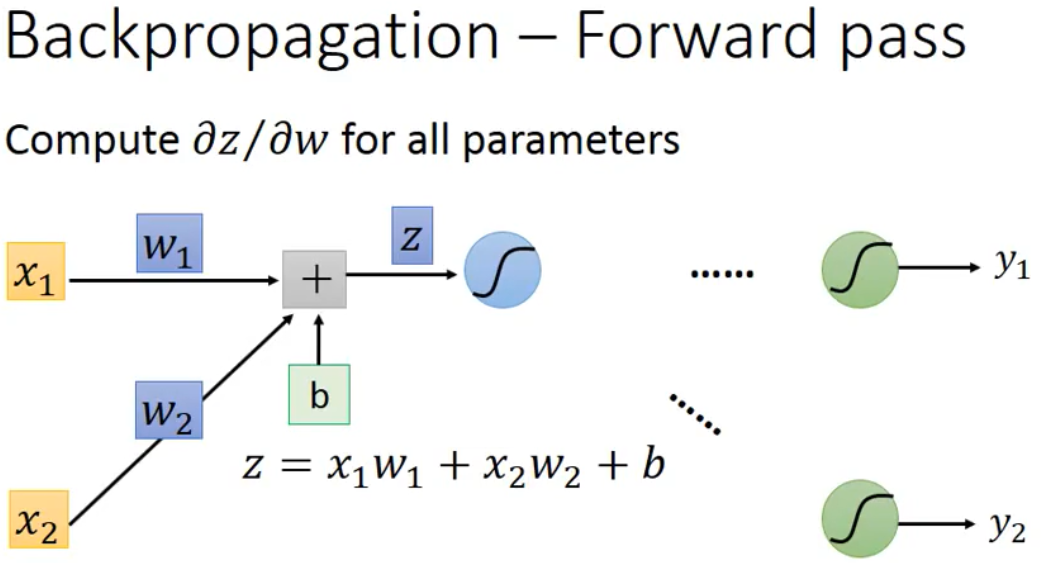
只讨论神经网络的一个节点。

$$
\frac{\partial C}{\partial w}=\frac{\part C}{\part z}\frac{\part z}{\part w}
$$
求z对w求导，很简单，对w1求导是x1，对w2求导是x2。

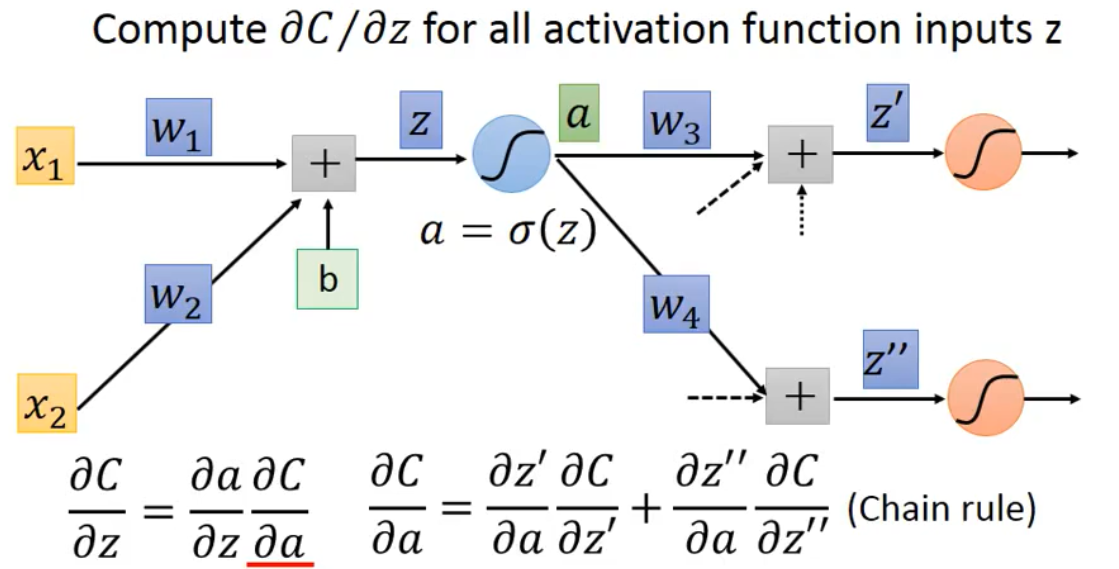
假设第二层神经节点的输入a，是将z通过一个信号函数(signal) $\sigma(z)$得到的现在求$\frac{\part C}{\part z}$
$$
\frac{\part C}{\part z}=\frac{\part a}{\part z}\frac{\part C}{\part a}
$$
利用链式法则，求$\frac{\part C}{\part a}$

公式见上图。此时，通过反向传递法则。假设红色的信号节点就是神经网络的最后一个节点，对应输出就是神经网络输出。那么可以倒推回去。$\frac{\part C}{\part z^,}$就等于最后的sign函数导数。因此能求得$\frac{\part C}{\part a}$，这样依次反推回去。最终求得每个节点的$\frac{\part C}{\part z}$。从而求得Loss function的导数。

第八章 Tips for Deep Learning

定义一个方程
方程好坏
选择最好的方程
获得一个Neural Network
是否获得一个好的结果在Training Data，如果不好重新选择最好的方程
在Testing Data获得不好的结果，overfitting，则重新定义一个方程。

ReLU

Rectified Linear Unit.矫正线性单元

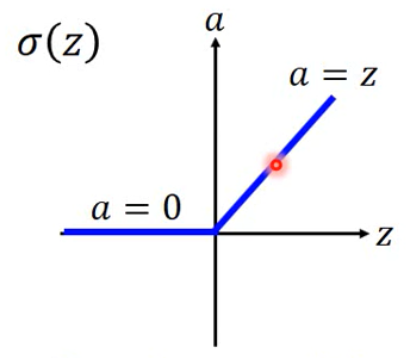
如果某个节点，输出是零，那么他对最后的结果没有任何影响。所以，输出为零关联的之后节点都可以被拿掉。

ReLU -variant

当z小于0时，a=mz。

Leaky ReLU ：m=0.01

Parametric: m可变

Maxout

最大输出，将不同输入的输出z分组，组内选出最大的值，作为下一个节点输入。

RMSProp
$$
w^1 \leftarrow w^0-\frac{\eta}{\sigma^0}g^0 \ \ \ \ \ \sigma^0=g^0
\
w^2 \leftarrow w^1-\frac{\eta}{\sigma^1}g^1 \ \ \ \ \ \sigma^1=\sqrt{\alpha (\sigma^0)^2+(1-\alpha)(g^1)^2}
\……
$$
$\alpha$可以设置。

Momentum

在初始点$\theta^0$处，加速度方向为gradient方向。

初始移动距离:$v_0=0$

加速度(第一点处的gradient):$\triangledown L(\theta^0)$

移动距离:$v^1=\lambda v^0-\eta \triangledown L(\theta^0)$

移到第二点:$\theta^1=\theta^0+v^1$

计算第二点的加速度:$\triangledown L(\theta^1)$

下一次移动距离:$v^2=\lambda v^1-\eta \triangledown L(\theta^1)$

移动到第三点:$\theta^2=\theta^1+v^2$

Adam:RMSProp+Momentum

过拟合问题

early stop

通过情况可能出席，当训练集增加时，测试集的正确率反而下降，因此通过减少训练集的数据来达到防止过拟合。

Regularization

$$
L^,(\theta)=L(\theta)+\lambda \frac{1}{2}||\theta||_2
$$

$$
||\theta||_2=(w_1)^2+(w_2)^2+……
$$

$||\theta||_2$不考虑biases，因为正则化是为了让loss function更加平滑，biases并不会起到作用。

Loss function求导:
$$
\frac{\partial L^,}{\partial w}=\frac{\partial L}{\part w}+\lambda w
$$
在找下一个
$$
w^{t+1}\rightarrow w^t-\eta\frac{\part L^,}{\part w} =w^t-\eta(\frac{\part L}{\part w}+\lambda w^t)=(1-\eta\lambda)w^t-\eta\frac{\part L}{\part w}
$$

Dropout

在更新参数之前：

每个节点有p%几率被丢掉
使用新的网络去训练

测试时：

没有丢弃节点

如果丢弃率为p%，所有的weights times(1-p)%

可以理解为，在训练时，腿上绑重物，测试时把重物拿掉。

为什么要乘(1-p)%

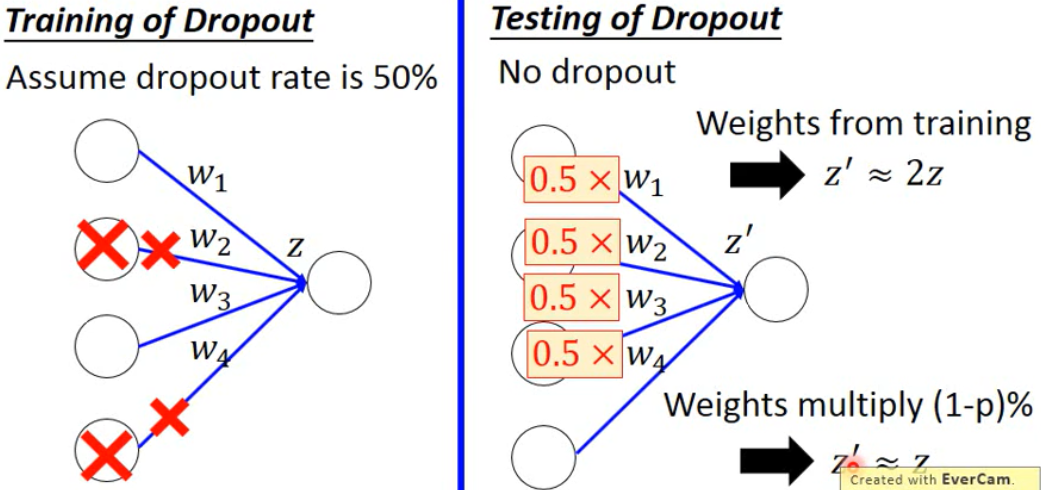
假设丢弃率为50%,在训练时一半节点被拿掉，而测试时使用了所有节点，导致节点z相差两倍，在测试时将所有weight乘50%，保证测试时的$z’\approx z$

第八章 Why deep

矮胖？高瘦？

实验数据表明，相同参数情况下，deep的错误率更小。

Modularization

Deep->Modularization

比如辨别男生长发、男生短发、女生长发、女生长发。

男生长发的训练集是很少的。

使用模组化，可以先辨别性别，在辨别头发长短。这样性别和长短发的训练集都是差不多的。这样男生长发也有好的正确率。

Deep->Modularization->Less training data

Modularization-Speech

人类语言的架构

Phoneme:人类发音的音节，

Tri-phone:不同的组合

State: 不同的节

语音识别：

分类：input->acoustic feature,output->state

deep的好处是，可以把复杂的问题，使用很多个简单的function连接在一起。

第九章 Pytorch

指定设备，迁移到某个设备

cpu = torch.device("cpu")
gpu=torch.device("gpu")
x= torch.rand(10)
print(x)
x=x.to(gpu)

更新于：2021年2月20日

机器学习

ShopXO商城优化-商城后台、小程序、飞鹅订单打印、公众号新订单推送

1：内容梗概ShopXO是款非常优秀的开源商城软件。为了让商城更加适合没有网站管理经验的人使用，我优化了手机和电脑端的商城后台。修复了小程序的一些BUG，并做了一些其他优化。使用飞鹅打印机，接收...

计算机网络技术学习笔记

1：基础概念局域网、城域网、广域网的区别实训任务：宽带城域网的逻辑结构，“三个平台一个出口” 管理平台、业务平台、网络平台（核心层、汇聚层、接入层）、城市宽带出口- 核心层：为汇...