北大人工智能实践——TensorFlow2

Qifei
学习笔记

发布于：2020年11月12日
次浏览

1：人工智能三学派

  • 准备数据
  • 搭建网络
  • 优化参数
  • 应用网络

2：神经网络设计过程

鸢尾花的分类：

通过测量花萼长、花萼宽。

if语句case语句——专家系统把专家的经验告知计算机，计算机执行逻辑判断。给出分类

神经网络：采集大量数据对构成数据集。

3：张量生成

张量（Tensor）：多维数组（列表） 阶：张量的维数

阶 名字 例子
0 标量 S=1 2 3
1 向量 v=[1,2,3]
2 矩阵
n 张量

创建张量

1
2
3
4
a = tf.constan(张量内容,dtype = 数据类型)
print(a)
print(a.dtype)
print(a.shape)
1
2
3
4
tf.zeros(维度)
tf.ones(维度)
tf.fill(维度，指定值)
c = tf.fill([2,2],9)	//两行两列
1
2
3
tf.random.normal(维度,mean=均值,stddev=标准差)
tf.random.truncated_normal(维度，mean=均值,stddev=标准差)
tf.random.uniform(维度,minval=最小值,maxval=最大值)

4：常用函数

1
2
3
tf.cast(张量名,dtype=数据类型)	//强制转换数据类型
tf.reduce_min()	//计算最大值
tf.reduce_max()
1
2
tf.reduce_mean(张量名,axis=操作轴)	//计算张量延指定维度平均值
tf.reduce_sum(张量名,axis=操作轴)	//计算沿指定维度的和

未指定操作轴，则为对全部数进行操作

变量：

1
tf.Variable(初始值)

数学运算

1
2
3
4
5
6
7
8
tf.add()
tf.subtract()
tf.multiply()
tf.divide()
//只有维度相同才能进行四则运算
tf.square(张量名)	平方
tf.pow()	//n次方
tf.sqrt()	//开方

矩阵乘

1
tf.matmul(矩阵1，矩阵2)

特征和标签对应：

1
2
3
features = tf.constant([12,23,10,14])
labels = tf.constant([0,1,1,0])
dataset = tf.data.Dataset.from_tensor_slices((features,labels))

计算梯度

1
2
3
4
with tf.GradientTape() as tape:
	w = tf.Variable(tf.constant(3.0))
	loss = tf.pow(w,2)
grad = tape.gradient(loss,w)

enumerate

1
2
3
seq = ['one','two','three']
for i,element in enumerate(seq):
	print(i,element)

独热编码：

标记类别：1表示是，0表示否

1
tf.one_hot(待转换数据，depth=几分类)

输出符合概率分布：

1
2
3
4
tf.nn.softmax(x)

y = tf.constant([1.01,2.01,-0.66])
y_pro = tf.nn.softmax(y)

参数自更新：

1
2
3
w = tf.Variable(4)
w.assign_sub(1)	//w-=1
print(w)

返回最大值索引

1
tf.argmax(张量名，axis=操作轴)

条件语句：

1
tf.where(条件语句,真返回A,假返回B)

返回[0,1)之间的随机数

1
np.random.RandomState.rand(维度)

将两个数组按垂直方向叠加（一维—>二维）：

1
np.vstack(数组1，数组2)
1
2
3
4
5
x,y = np.mgrid[1:3:1,2:4:0.5]	//x=[[1 1 1 1]
                                     [2 2 2 2]]
									y=[[2 2.5 3 3.5]
                                       [2 2.5 3 3.5]] 
gird = np.c_[x.ravel(),y.ravel()]	//ravel()降维到一维，np.c_[数组1，数组2]配对。

5：神经网络(NN)复杂度

NN复杂度：多用NN层数和NN参数的个数表示。

  • 空间复杂度
  • 时间复杂度

学习率:
$$
w_{t+1} = w_t+lrgradient
$$
指数衰减学习率:
$$
指数衰减学习率=初始学习率学习率衰减率^{当前轮数/多少轮衰减一次}
\\epoch= 40
\\LR_BASE= 0.2
\\LR_DECAY= 0.99
\\LR_STEP=1
$$

1
2
3
4
5
6
for epoch in range(epoch):
    lr = LR_BASE*LR_DECAY**(epoch/LR_STEP)
    with tf.GradientTape() as tape:
        loss = tf.square(w+1)
    grads = tape.gradient(loss,w)
    w.assign_sub(lr*grads)

6：激活函数

$$
y = f(wx+b)
$$

  • Sigmoid函数

$$
f(x)=\frac{1}{1+e^{-x}}
$$

1
tf.nn.sigmoid(x)

易造成梯度消失

输出非0均值，收敛慢

幂运算复杂，训练时间长

  • Tanh函数

$$
f(x) = \frac{1-e^{-2x}}{1+e^{-2x}}
$$

1
tf.math.tanh(x)
  • Relu函数

$$
\begin{align}
f(x)=& max(x,0)
\\=& \begin{cases}
0\qquad x<0\
x\qquad x>=0
\end{cases}
\end{align}
$$

1
tf.nn.relu(x)
  • Leaky Relu函数

$$
f(x)=max(ax,x)
$$

1
tf.nn.leaky_relu(x)

初学者：

  • 首选Relu函数
  • 学习率设置较小值
  • 输入特征标准化，让输入特征满足以0为均值，1为标准差的正态分布
  • 初始参数中心化，让随机生成的参数满足以0为均值，sqrt(2/当前层输入特征个数)为标准差的正态分布

7：损失函数

loss：预测值(y)与已知答案(y_)的差距

  • 均方误差mse：

$$
MSE(y_,y)=\frac{\sum^n_{i=1}(y-y_)^2}{n}
$$

1
loss_mse = tf.reduce_mean(tf.square(y-y_))
  • 自定义损失函数

y_:标准答案

y:预测答案
$$
f(y_,y)=\begin{cases}
PROFIT*(y_-y)\quad y<y_ \ 预测的y少了，损失利润
\COST*(y-y_)\quad y>=y_ \ 预测的y多了，损失成本
\end{cases}
$$

1
loss_diy = tf.reduce_sum(tf.where(tf.greater(y,y_),COST(y-y_),PROFIT(y_-y)))	//y>y_?,为真COST，为假PROFIT
  • 交叉熵损失函数CE：表征两个概率分布之间的距离

$$
H(y_,y)=-\sum y_*lny
$$

1
tf.losses.categorical_crossentropy(y_,y)
  • softmax和交叉熵结合

softmax计算概率分布

1
tf.nn.softmax_cross_entropy_with_logits(y_,y)

8：缓解过拟合

  • 正则化缓解过拟合

正则化在损失函数中引入模型复杂度指标，利用给W加权值，弱化训练数据的噪声。

$$
loss=loss(y与y_)+REGULARIZER*losss(w)
$$

L2正则化

1
2
3
4
5
6
7
8
9
10
11
with tf.GradientTape() as tape:
	h1 = tf.matmul(x_train,w1)+b1
	h1 = tf.nn.relu(h1)
	y = tf.matmul(h1,w2) + b2
	loss_mse = tf.reduce_mean(tf.square(y_train - y))
	loss_regularization = []
	loss_regularization.append(tf.nn.l2_loss(w1))
	loss_regularization.append(tf.nn.l2_loss(w2))
	loss_regularization = tf.reduce_sum(loss_regularization)
	loss = loss_mse + 0.03*loss_regularization

9：优化器

$m_t$：一阶动量(与梯度相关的函数) $V_t$：二阶动量(与梯度平方相关的函数)

下降梯度$\eta_t=lr*m_t/\sqrt{V_t}$

更新参数$w_{t+1}=w_t-\eta_t$

不同的优化器，只是定义了不同的动量函数

  • SGD，梯度下降法

$m_t=g_t$ $V_t=1$

$w_{t+1}=w_t-lr*g_t$

  • SGDM，SGD基础上增加了一阶动量

$m_t=\beta*m_{t-1}+(1-\beta)*g_t$

$V_t=1$

  • Adagrad，在SGD基础上增加二阶动量

$m_t=g_t$

$V_t=\sum^t_{\tau=1}g^2_\tau$

  • RMSProp，SGD基础上增加二阶动量

$m_t=g_t$

$V_t=\beta*V_{t-1}+(1-\beta)*g^2_t$

  • Adam，同时结合SGDM一阶动量和RMSProp二阶动量

$m_t=\beta*m_{t-1}+(1-\beta)*g_t$

修正一阶动量的偏差：$\hat{m_t}=\frac{m_t}{1-\beta^t_1}$

$V_t=\beta*V_{t-1}+(1-\beta)*g^2_t$

修正二阶动量的偏差：$\hat{V_t}=\frac{V_t}{1-\beta^t_2}$

10：搭建八股网络-Sequential

tf.keras搭建网络八股

六步法：

  1. import
  2. train,test
  3. model = tf.keras.models.Sequential
  4. model.compile
  5. model.fit
  6. model.summary
  • Sequential，描述各层网络

拉直层：tf.keras.layers.Flatten()

全连接层：tf.keras.layers.Dense(神经元个数,activation=”激活函数”,kernel_regularizer=哪种正则化)

activation：relu、softmax、sigmoid、tanh

kernel_regularizer：tf.keras.regularizers.l1()、tf.keras.regularizers.l2()

卷积层：tf.keras.layers.Conv2D(filters = 卷积核个数,kernel_size = 卷积核尺寸,strides = 卷积步长,padding = “valid”or”same”)

LSTM层：tf.keras.layers.LSTM()

  • Compile
1
model.compile(optimizer = 优化器,loss=损失函数,metrics=["准确率"])
  • Fit
1
model.fit(训练集的输入特征，训练集的标签，bathc_size=,epochs=,validation_data=(测试集的输入特征，测试集的标签)，validation_split=从训练集划分多少比例给测试集，validation_freq=多少次epoch测试一次)
  • Summary
1
model.summary()

11：搭建网络八股-class

1
2
3
4
5
6
7
8
9
class MyModel(Model):
	def __init__(self):
		super(MyModel,self).__init__()
        定义网络结构块
    def call(self,x):
        调用网络结构块，实现前向传播
        reutrn y
        
 model = MyModel()

12：MNIST数据集

提供6万张28*28像素点的0-9手写数字图片和标签，用于训练

1万张28*28像素点的0-9手写数组图片和标签，用于测试

  • 导入MNIST数据集
1
2
mnist = tf.keras.datasets.mnist
(x_train,y_train),(x_test,y_test)=mnist.load_data()
  • 作为输入特征，将数据拉伸为一维数组
1
tf.keras.layers.Flatten()

13：Fasion_MNIST数据集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import tensorflow as tf

fasion = tf.keras.datasets.fashion_mnist
(x_train, y_train),(x_test,y_test) = fasion.load_data()
x_train,x_test = x_train/255.0,x_test/255.0

model = tf.keras.models.Sequential([
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(128,activation='relu'),
    tf.keras.layers.Dense(10,activation = 'softmax')
])

model.compile(optimizer="adam",loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),metrics=['sparse_categorical_accuracy'])
model.fit(x_train,y_train,batch_size = 32,epochs=5,validation_data=(x_test,y_test),validation_freq = 1)
model.summary()

14：自制数据集

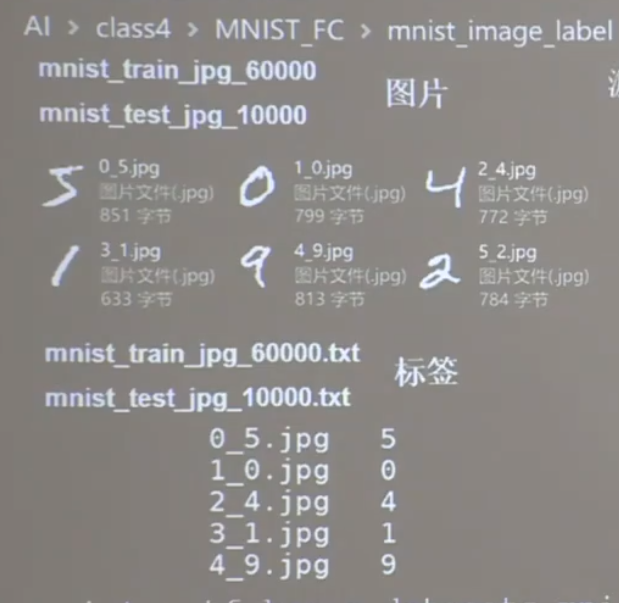
在mnist_image_label文件夹下有两个文件夹mnist_train_jpg_60000和mnist_test_jpg_10000

每个文件夹分别放了对应个数的图片以及一个.txt文件，文件内容如上，jpg名+空格+标签

现在需要重写(x_train,y_train),(x_test,y_test)=mnist.load_data()中的load_data()方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def generateds(path,txt):
    f = open(txt,'r')
    contents = f.readlines()
    f.close()
    x,y_ = [],[]
    for content in contents:
        value = content.split()
        img_path = path+value[0]
        img = Image.open(img_path)
        img = np.array(img.convert('L'))
        img = img/255.
        x.append(img)
        y_.append(value[1])
        print('loading:'+content)
    x = np.array(x)
    y_ = np.array(y_)
    y_ = y_.astype(np.int64)
    return x,y_

保存数据集

1
np.save(保存路径带拓展,保存的内容)

15：数据增强

1
2
3
4
5
6
7
8
image_gen_train = tf.keras.preprocessing.image.ImageDataGenerator(
	rescale = 所有数据将乘以该数值
	rotation = 随机旋转角度值范围
    width_shift_range = 随机宽度偏移量
    height_shift_range = 随机高度偏移量
    horizontal_flip = 是否随机水平翻转
    zoom_range = 随机缩放的范围[1-n,1+n])
image_gen_train.fit(x_train)

fit()中的数据是四位数据，所以需要对其reshape

x_train = x_train.reshape(x_train.shape[0],28,28,1)

最后的1表示灰度值。

model.fit()方法内修改为

1
model.fit(image_gen_train.flow(x_train,y_train,batch_size = 32),epochs=5,validation_data=(x_test,y_test),validation_freq = 1)

16：断点续训

读取模型：

load_weights(路径文件名)

1
2
3
4
checkpoint_save_path = "./checkpoint/mnist.ckpt"
if os.path.exists(checkpoint_save_path + '.index')
	print('-----load the model------')
    model.load_weights(checkpoint_save_path)

保存模型

1
2
3
4
5
callback = tf.keras.callbacks.ModelCheckpoint(
	filepath = 路径文件名,
	save_weights_only=True/False,
	save_best_only = True/False)
history = model.fit(……callbacks = [cp_callback])

17：参数提取

model.trainable_variables 返回模型中可训练的参数

设置print输出格式

1
np.set_printoptions(threshold = 超过多少省略显示)	#threshold=np.inf表示无限
1
2
3
4
5
6
7
8
np.set_printoptions(threshold = np.inf)
print(model.trainable_variables)
file = open('./weights.txt','w')
for v in model.trainable_variables:
	file.write(str(v.name)+'\n')
    file.write(str(v.shape)+'\n')
    file.write(str(v.numpy())+'\n')
file.close()

18：acc曲线和loss曲线可视化

1
2
3
4
5
history = model.fit()
acc = history.history['sparse_categorical_accuracy']	#训练集准确率
val_acc = history.history['val_sparse_categorical_accuracy']	#测试集准确率
loss = history.history['loss']	#训练集loss
val_loss = history.history['val_loss']	#测试集loss

画图

1
2
3
4
5
6
7
8
9
10
11
12
plt.subplot(1,2,1)
plt.plot(acc,label="Training Accuracy")
plt.plot(val_acc,label="Validation Accuracy")
plt.title("Training and Validation Accuracy")
plt.legend()

plt.subplot(1,2,2)
plt.plot(loss,label="Training Loss")
plt.plot(val_loss,label="Validation Loss")
plt.title('Training and Validation Loss')
plt.legend()
plt.show()

19：样例预测

predict(输入特征,batch_size=整数)

1
2
3
4
5
6
7
8
9
#复现模型
model = tf.keras.models.Sequential([
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(128,activation = 'relu'),
    tf.keras.layers.Dense(10,activation = 'softmax')])
#加载参数
model.load_weights(model_save_path)
#预测结果
result = model.predict(x_predict)

20：卷积计算过程

原始彩色图片——>若干层特征提取——>全连接网络

主要模块：(CBAPD)

卷积(Convolutional)->批标准化(BN)->激活(Activation)->池化(Pooling)->舍弃(Dropout)

21：感受野

感受野：卷积神经网络各输出特征图中的每个像素点，在原始输入图片上映射区域的大小。

比如：

1：

5x5原始图，使用3x3卷积核，生成的3x3特征图，那么其感受野是3.

将生成的3x3特征图，再次使用3x3卷积核作用，生成1x1特征图，那么这个特征图相对于原始图，感受野为5.

2：

5x5原始图，使用5x5卷积核，生成1x1特征图，其感受野同样为5

长款x大于10时，两层3x3卷积核性能优于一层5x5卷积核

22：全零填充

特征图一圈填充零。

特征图边长
$$
padding=\begin{cases}
SAME(全0填充)\ \frac{入长}{步长}\ (向上取整)
\VALID(不全0填充)\ \frac{入长-核长+1}{步长}\ (向上取整)
\end{cases}
$$

23：描述卷积层

1
2
3
4
5
6
7
8
tf.keras.layers.Conv2D(
	filter = 卷积核个数,
    kernel_size = 卷积核尺寸，	#正方形写核长整数，或（核高，核宽）
    strides = 滑动步长,	#横纵相同写步长整数，或（纵向步长，横向步长）
    padding = "same" or "valid"	#全零填充same，非全零valid
    activation = "relu" or "sigmoid",
    input_shape = (高，宽，通道数)	#输入特征图维度，可省
)

24：批标准化（Batch Normalization）

标准化：使数据符合0均值，1为标准差的分布

批标准化：对一小批数据，做标准化
$$
H’^k_i = \frac{H^k_i-\mu^k_{batch}}{\sigma_{batch}^k}
$$
k：第k个卷积核

i：第i个像素点

H’：批标准化之后

H：批标准化之前

上述式子，要求批标准化之前的特征数据即满足正态分布。

通常使用：
$$
x^k_i=\gamma_kH’^k_i+\beta_k
$$
$\gamma_k$:缩放因子

$\beta_k$:偏移因子

调整分布的宽窄和偏移。

BN层位于，卷积层之后，激活层之前。

1
tf.keras.layers.BatchNormalization()

25：池化

池化用于减少特征数据量。

最大池化，均值池化

1
2
3
4
5
6
tf.keras.layers.MaxPool2D(
	pool_size=池化核尺寸
	strides=池化步长
	padding='valid' or 'same'	#全零填充？
)
tf.keras.layers.AveragePooling2D()

26：舍弃（dropout）

在神经网络训练时，将一部分神经元按照一定概率从神经网络中暂时舍弃，神经网络使用时，被舍弃的神经元恢复连接。

1
tf.keras.layers.Dropout(舍弃概率)

27：Cifar10数据集

五万张32*32像素点的是分类彩色图片和标签，用于训练

测试1万张

28：LeNet

输入：32*32

相关文章
Bootstrap学习笔记

博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本文永久链接是：https://blog.sci.ci/2020/11/12/%E5%8C%97%E5%A4%A7%E4%BA%BA%E5%B7%A5%E6%99%BA%E8%83%BD%E5%AE%9E%E8%B7%B5%E2%80%94%E2%80%94TensorFlow2/

更新于：2021年2月20日

人工智能

评论