1：什么是激活函数
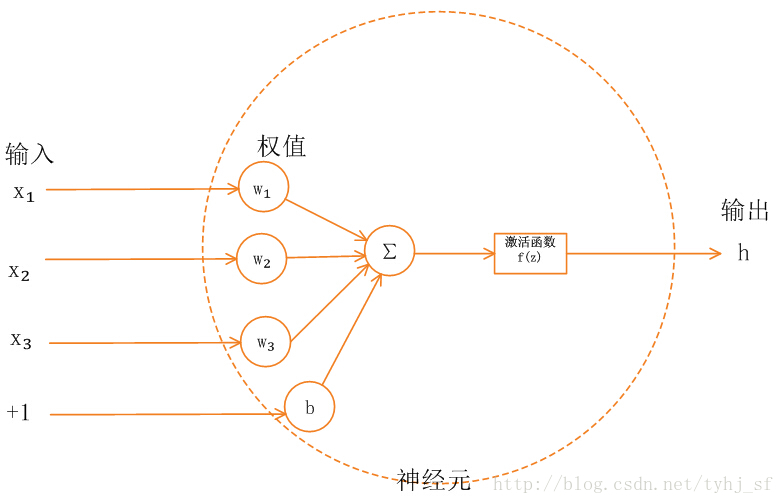
以一个简单的神经元为例。在没有激活函数时，神经元输出z等于$z=x_1w_1+x_2w_2+x_3w_3+b$
而激活函数将z作为输入，得到新的神经元输出$f(z)$
这里的$f(z)$即激活函数。激活函数的主要作用是使输出非线性化，即曲线化或者分段化（对应分段函数）。
2：为什么要激活函数
从$z=x_1w_1+x_2w_2+x_3w_3+b$不难看出，在没有激活函数时，我们的神经元输出，总是与输入$x_1,x_2,x_3$成线性关系。。
简单点的例子，$z = x_1*w+b$。
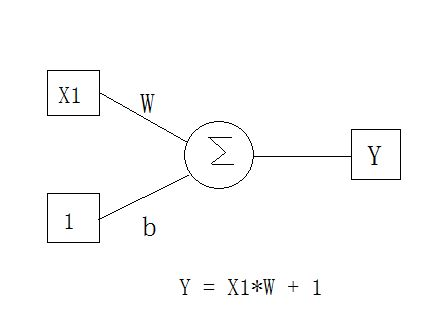
可以知道，这是一条直线。可以解决一个简单的二分类问题。
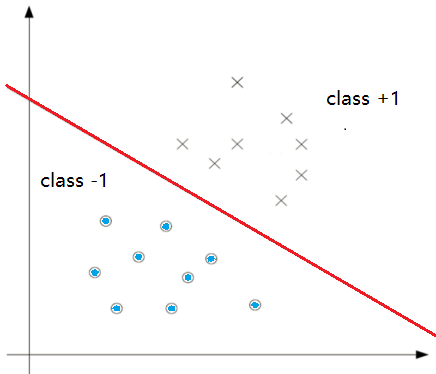
如果这个二分类不是用直线分割的呢？
比如，一个圆形，圆内的点是1，圆外是0。我们用直线就很难将他们区分开了。
当然，也可以使用无数条小的直线来划分这两个区域，但是对比直接使用曲线，就复杂多了。
为了让我们的输出函数，符合非线性特征，引入了激活函数的概念。
3：哪些激活函数
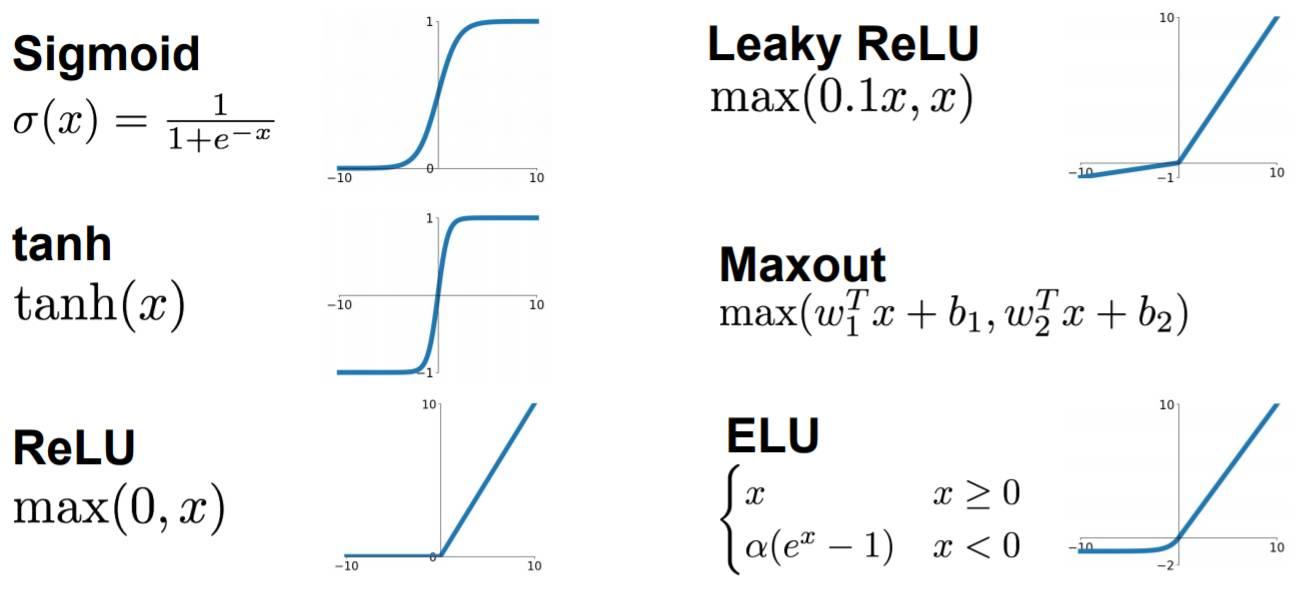
- Sigmoid函数
Sigmoid函数只会输出0到1之间的正数，当输入无穷小时，输出为0，输入无穷大时，输出为1。
缺点：
基于反向传播（根据链式求导法则）的参数更新，随着网络层数的增加，w更新的梯度会越来越小，并逐渐接近于零。也就是所谓的梯度消失。
下图是链式求导法则求w梯度的过程。这是某个神经网络中的一部分神经元。
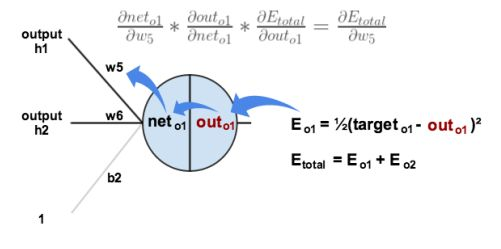
其中，$net_{o1}=h1w5+h2w6+b2$
$out_{o1}=Sigmoid(net_{o1})$
误差函数为$E_{o1}=\frac{target-out_{o1}}{2}$
获得$w_5$更新所需的梯度就是求$E_{o1}$对$w_5$求导。
根据链式法则，
$$
\frac{\partial E_{o1}}{\part w_5} = \frac{\part E_{o1}}{\part out_{o1}}* \frac{\part out_{o1}}{\part net_{o1}}* \frac{\part net_{o1}}{\part w_5}
$$
其中$\frac{\part out_{o1}}{\part net_{o1}}$就是Sigmoid函数求导。
根据Sigmoid函数求导公式，
$$
\frac{\part g(z)}{\part z} = g(z)(1-g(z))
$$
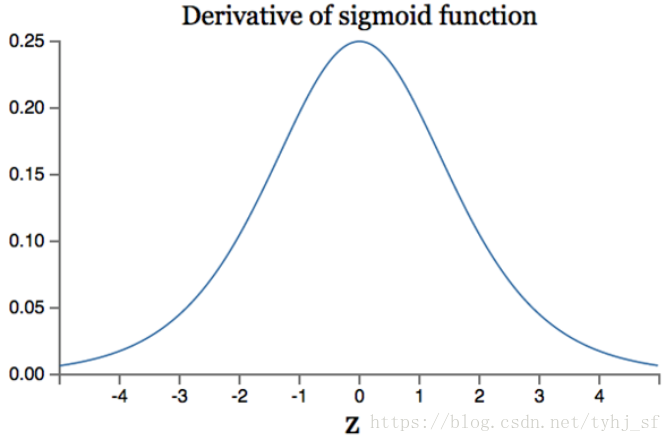
上式，$g(z)$为Sigmoid函数，其导数最大值为0.25.
当神经元个数逐渐增多，前向w梯度，是后向w梯度做链式法则的结果，那么会有许多个$g’(z)$相乘。则，前向w的梯度会逐渐趋近于0。
- tanh函数
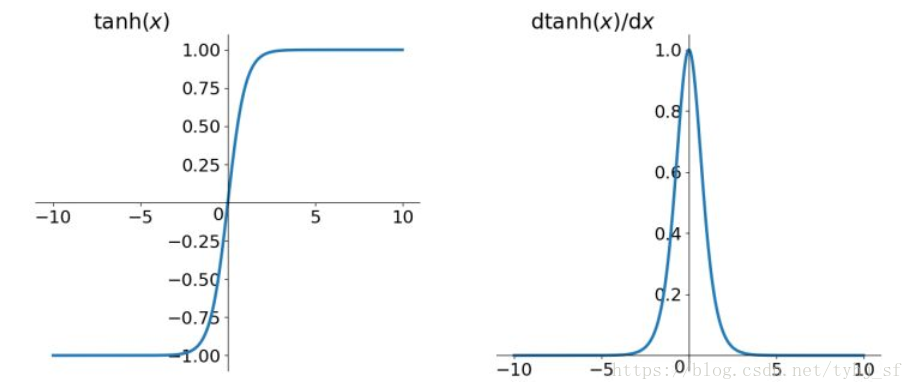
相比于Sigmod函数，其输出均值为0。
缺点：
仍然存在梯度消失现象。
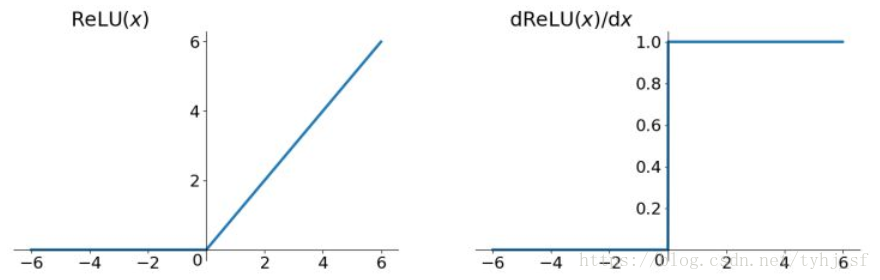
- Relu函数
目前最常用的函数，只需判断输入是否大于零，小于零的输入，输出为0
4：参考资料
《CNN入门讲解：什么是激活函数（Activation Function）》
博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议
